Introduction
Given the large amount of data to be summarized, the use of graphics
are an integral component of representing the results. Pruzek and
Helmreich (2009) introduced a class of graphics for visualizing
dependent sample tests (see also Pruzek & Helmreich, 2010; Danielak,
Pruzek, Doane, Helmreich, & Bryer, 2011). This framework was then
extended for propensity score methods using stratification (Helmreich
& Pruzek, 2009). In particular, the representation of confidence
intervals relative to the unit line (i.e. the line y=x) provided a new
way of determining whether there is a statistically significant
difference between two groups. The multilevelPSA package
provides a number of graphing functions that extend these frameworks for
multilevel PSA. The figure below represents a multilevel PSA assessment
plot with annotations. This graphic represents the results of comparing
private and public schools in North America using the Programme of
International Student Assessment (PISA; Organisation for Economic
Co-Operation and Development, 2009). The PISA data to create this
graphic are included in the multilevelPSA package and a
more detailed description of how to create this graphic are discussed in
the next section. Additionally, the use of PISA makes more visible
certain features of the graphics used. As discussed in chapters four and
five, the differences between charter and traditional public schools is
minimal and therefore some features of the figures are less apparent.
The following section focuses on the features of this graphic.
In the figure below, the x-axis corresponds to math scores for private schools and the y-axis corresponds to public school maths cores. Each colored circle (a) is a country with its size corresponding to the number of students sampled within each country. Each country is projected to the lower left, parallel to the unit line, such that a tick mark is placed on the line with slope -1 (b). These tick marks represent the distribution of differences between private and public schools across countries. Differences are aggregated (and weighted by size) across countries. For math, the overall adjusted mean for private schools is 487, and the overall adjusted mean for public schools is 459 and represented by the horizontal (c) and vertical (d) blue lines, respectively. The dashed blue line parallel to the unit line (e) corresponds to the overall adjusted mean difference and likewise, the dashed green lines (f) correspond to the confidence interval. Lastly, rug plots along the right and top edges of the graphic (g) correspond to the distribution of each country’s overall mean private and public school math scores, respectively.
The figure represents a large amount of data and provides insight into the data and results. The figure provides overall results that would be present in a traditional table, for instance the fact that the green dashed lines do not span the unit line (i.e. y = x) indicates that there is a statistically significant difference between the two groups. However additional information is difficult to convey in tabular format. For example, the rug plots indicate that the spread in the performance of both private and public schools across countries is large. Also observe that Canada, which has the largest PISA scores for both groups, also has the largest difference (in favor of private schools) as represented by the larger distance from the unit line.
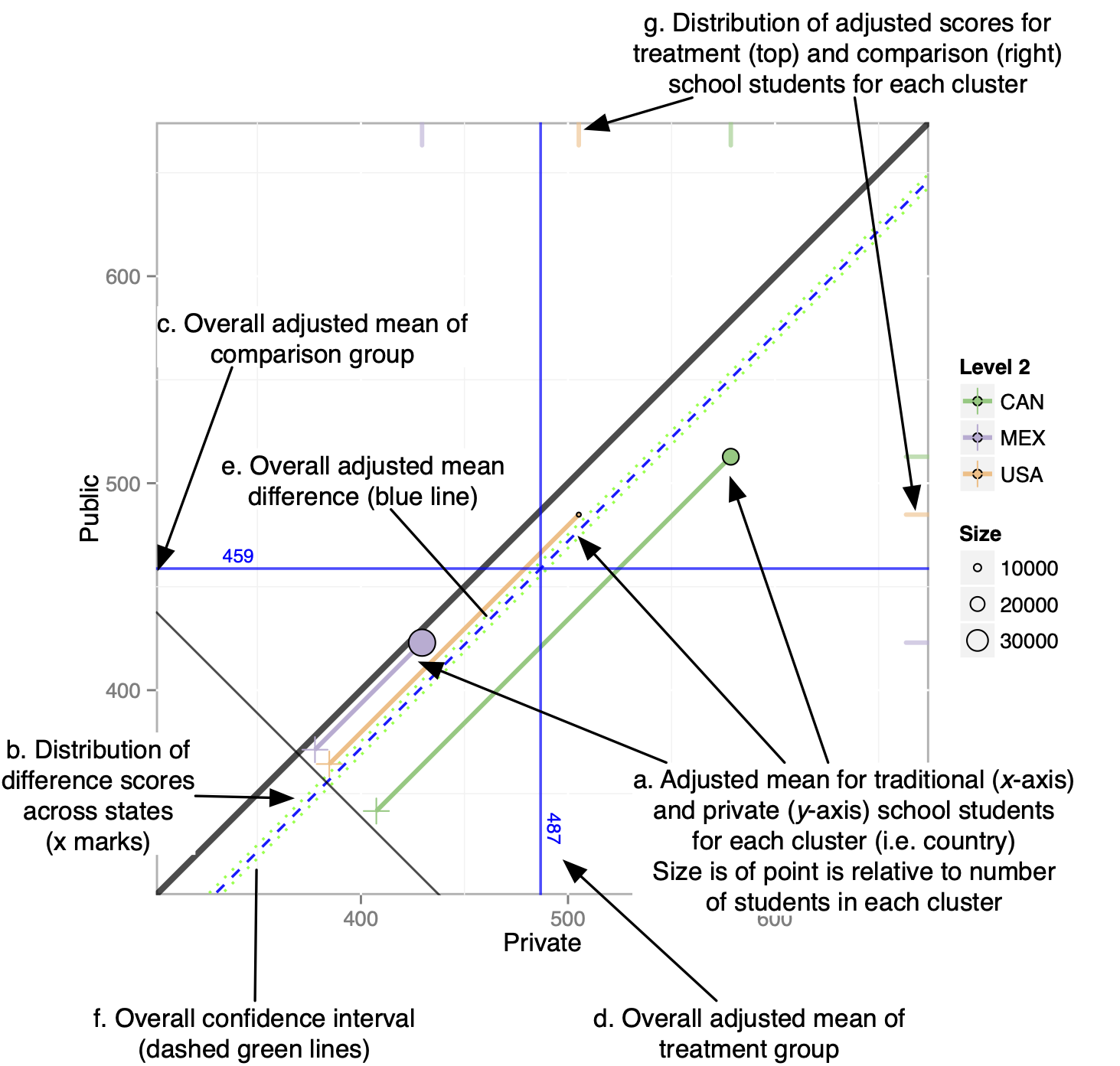
Annotated multilevel PSA assessment plot. This plot compares private schools (x- axis) against public schools (y-axis) for North America from the Programme of International Student Assessment.
Working Example
The multilevelPSA package includes North American data
from the Programme of International Student Assessment (PISA;
Organisation for Economic Co-Operation and Development, 2009). This data
is made freely available for research and is utilized here so that the R
code is reproducible9. This example compares the performance of private
and public schools clustered by country. Note that PISA provide five
plausible values for the academic scores since students complete a
subset of the total assessment. For simplicity, the math score used for
analysis is the average of these five plausible scores.
data(pisana)
data(pisa.psa.cols)
pisana$MathScore <- apply(pisana[,paste0('PV', 1:5, 'MATH')], 1, sum) / 5The mlpsa.ctree function performs phase I of the
propensity score analysis using classification trees, specifically using
the ctree function in the party package. The getStrata
function returns a data frame with a number of rows equivalent to the
original data frame indicating the stratum for each student.
mlpsa <- mlpsa.ctree(pisana[,c('CNT', 'PUBPRIV', pisa.psa.cols)],
formula = PUBPRIV ~ .,
level2 = 'CNT')
mlpsa.df <- getStrata(mlpsa, pisana, level2 = 'CNT')Similarly, the mlpsa.logistic estimates propensity
scores using logistic regression. The getPropensityScores
function returns a data frame with a number of rows equivalent to the
original data frame.
mlpsa.lr <- mlpsa.logistic(pisana[,c('CNT', 'PUBPRIV', pisa.psa.cols)],
formula = PUBPRIV ~ .,
level2 = 'CNT')
mlpsa.lr.df <- getPropensityScores(mlpsa.lr, nStrata = 5)
head(mlpsa.lr.df)
#> level2 ps strata
#> 1 CAN 0.92 2
#> 2 CAN 0.94 3
#> 3 CAN 0.97 4
#> 4 CAN 0.93 2
#> 5 CAN 0.84 1
#> 6 CAN 0.97 4The covariate.balance function calculates balance
statistics for each covariate by estimating the effect of each covariate
before and after adjustment. The results can be converted to a data
frame to view numeric results or the plot function provides
a balance plot. This figure depicts the effect size of each covariate
before (blue triangle) and after (red circle) propensity score
adjustment. As shown here, the effect size for nearly all covariates is
smaller than the unadjusted effect size. The few exceptions are for
covariates where the unadjusted effect size was already small. There is
no established threshold for what is considered a sufficiently small effect
size. In general, I recommend adjusted effect sizes less than 0.1 which
reflect less than 1% of variance explained.
cv.bal <- covariate.balance(covariates = pisana[,pisa.psa.cols],
treatment = pisana$PUBPRIV,
level2 = pisana$CNT,
strata = mlpsa.df$strata)
head(as.data.frame(cv.bal))
#> covariate es.adj es.adj.wtd es.unadj
#> 1 (Intercept) 0.000 0.0e+00 NaN
#> 2 ST05Q01Yes, more than one year 0.097 2.3e-04 0.287
#> 3 ST05Q01Yes, one year or less 0.051 6.6e-05 0.220
#> 4 ST07Q01Yes, once 0.103 -1.1e-03 0.235
#> 5 ST07Q01Yes, twice or more 0.044 -3.7e-04 0.087
#> 6 ST10Q01<ISCED level 2> 0.030 -1.7e-04 0.171
plot(cv.bal)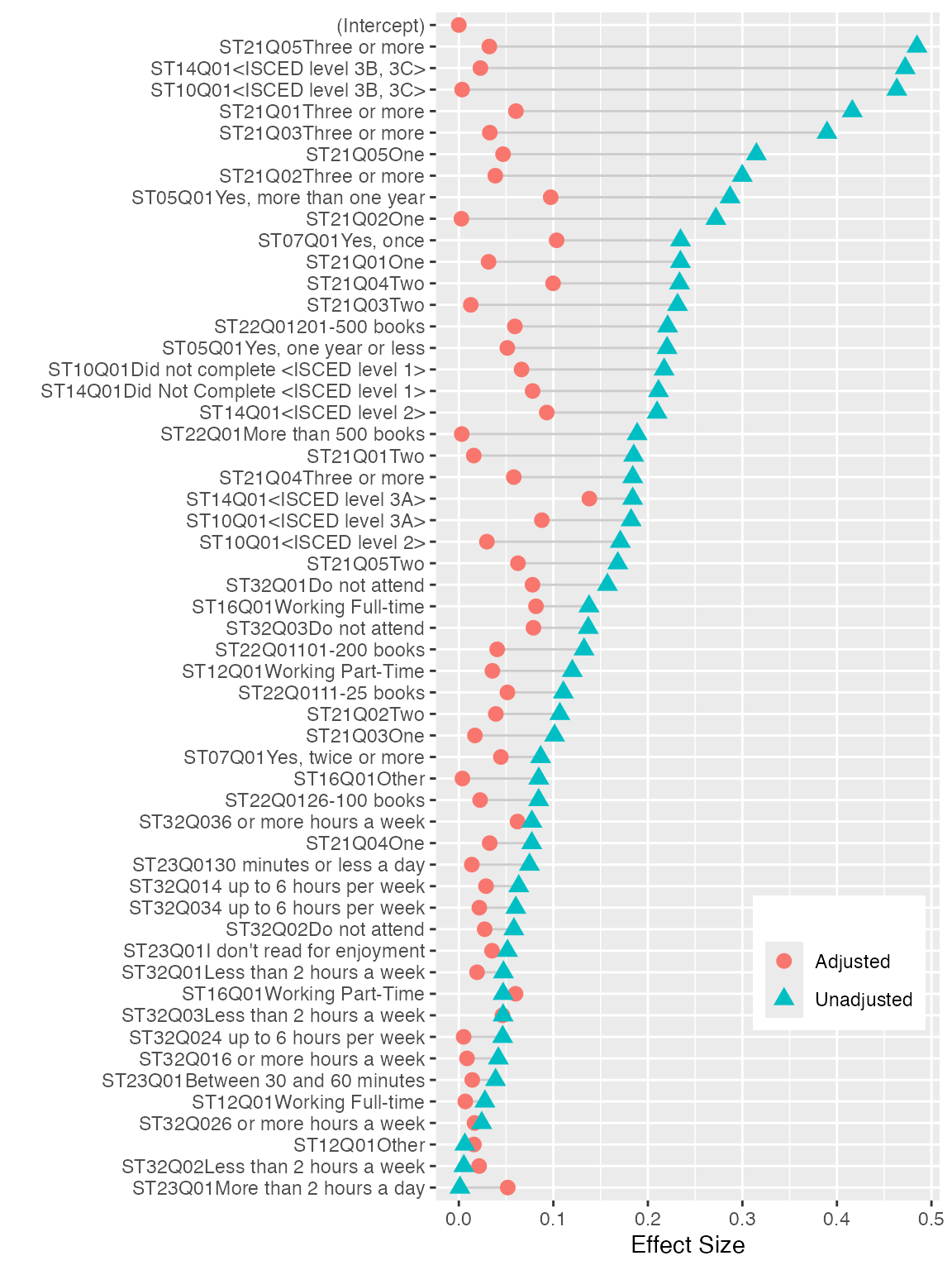
Multilevel PSA balance plot for PISA. The effect sizes (standardized mean differences) for each covariate are provided before PSA adjustment (blue triangles) and after PSA adjustment (red circles).
The mlpsa function performs phase II of propensity score
analysis and requires four parameters: the response variable, treatment
indicator, stratum, and clustering indicator. The minN
parameter (which defaults to five) indicates what the minimum stratum
size is to be included in the analysis. For this example, 463, or less
than one percent of students were removed because the stratum (or leaf
node for classification trees) did not contain at least five students
from both the treatment and control groups.
results.psa.math <- mlpsa(response = mlpsa.df$MathScore,
treatment = mlpsa.df$PUBPRIV,
strata = mlpsa.df$strata,
level2 = mlpsa.df$CNT)
#> Removed 463 (0.696%) rows due to stratum size being less than 5The summary function provides the overall treatment
estimates as well as level one and two summaries.
summary(results.psa.math)
#> Multilevel PSA Model of 85 strata for 3 levels.
#> Approx t: -10.8
#> Confidence Interval: -31.3, -24.75
#> level2 strata Treat Treat.n Control Control.n ci.min ci.max
#> 1 CAN Overall 579 1625 513 21093 -72 -59.6
#> 2 <NA> 1 580 28 492 1128 NA NA
#> 3 <NA> 2 600 9 476 1326 NA NA
#> 4 <NA> 3 585 11 513 630 NA NA
#> 5 <NA> 4 571 140 508 2240 NA NA
#> 6 <NA> 5 578 8 470 179 NA NA
#> 7 <NA> 6 500 19 447 310 NA NA
#> 8 <NA> 7 584 83 503 3276 NA NA
#> 9 <NA> 8 471 5 464 120 NA NA
#> 10 <NA> 9 560 41 526 190 NA NA
#> 11 <NA> 10 502 20 463 91 NA NA
#> 12 <NA> 11 557 44 517 750 NA NA
#> 13 <NA> 12 559 34 521 292 NA NA
#> 14 <NA> 13 562 8 489 475 NA NA
#> 15 <NA> 14 534 21 463 151 NA NA
#> 16 <NA> 15 585 126 520 2134 NA NA
#> 17 <NA> 16 566 25 533 245 NA NA
#> 18 <NA> 17 613 49 576 137 NA NA
#> 19 <NA> 18 563 57 527 659 NA NA
#> 20 <NA> 19 598 113 542 318 NA NA
#> 21 <NA> 20 629 15 562 143 NA NA
#> 22 <NA> 21 589 46 523 398 NA NA
#> 23 <NA> 22 594 99 548 194 NA NA
#> 24 <NA> 23 580 40 542 183 NA NA
#> 25 <NA> 24 581 52 539 342 NA NA
#> 26 <NA> 25 582 103 526 1219 NA NA
#> 27 <NA> 26 626 11 525 113 NA NA
#> 28 <NA> 27 589 35 516 804 NA NA
#> 29 <NA> 28 524 5 482 15 NA NA
#> 30 <NA> 29 551 12 527 348 NA NA
#> 31 <NA> 30 588 145 526 1195 NA NA
#> 32 <NA> 31 603 147 545 822 NA NA
#> 33 <NA> 32 528 27 528 7 NA NA
#> 34 <NA> 33 552 47 510 659 NA NA
#> 35 MEX Overall 430 4044 423 34090 -10 -3.1
#> 36 <NA> 1 516 83 485 13 NA NA
#> 37 <NA> 2 491 145 448 89 NA NA
#> 38 <NA> 3 494 151 475 178 NA NA
#> 39 <NA> 4 418 14 416 154 NA NA
#> 40 <NA> 5 454 127 438 484 NA NA
#> 41 <NA> 6 453 58 431 635 NA NA
#> 42 <NA> 7 496 247 487 293 NA NA
#> 43 <NA> 8 483 431 461 871 NA NA
#> 44 <NA> 9 472 6 467 110 NA NA
#> 45 <NA> 10 461 16 450 121 NA NA
#> 46 <NA> 11 481 285 470 696 NA NA
#> 47 <NA> 12 474 16 443 112 NA NA
#> 48 <NA> 13 405 33 413 943 NA NA
#> 49 <NA> 14 432 138 429 1484 NA NA
#> 50 <NA> 15 472 99 460 619 NA NA
#> 51 <NA> 16 445 78 438 898 NA NA
#> 52 <NA> 17 460 34 461 262 NA NA
#> 53 <NA> 18 460 113 455 367 NA NA
#> 54 <NA> 19 434 53 445 454 NA NA
#> 55 <NA> 20 458 69 446 367 NA NA
#> 56 <NA> 21 462 76 457 217 NA NA
#> 57 <NA> 22 477 93 452 150 NA NA
#> 58 <NA> 23 476 186 460 547 NA NA
#> 59 <NA> 24 477 10 437 130 NA NA
#> 60 <NA> 25 476 80 442 159 NA NA
#> 61 <NA> 26 437 167 428 1040 NA NA
#> 62 <NA> 27 436 146 435 1175 NA NA
#> 63 <NA> 28 442 45 429 406 NA NA
#> 64 <NA> 29 424 80 428 1963 NA NA
#> 65 <NA> 30 436 61 427 787 NA NA
#> 66 <NA> 31 426 48 428 645 NA NA
#> 67 <NA> 32 401 231 409 4314 NA NA
#> 68 <NA> 33 442 28 438 279 NA NA
#> 69 <NA> 34 424 34 426 1013 NA NA
#> 70 <NA> 35 420 63 427 2364 NA NA
#> 71 <NA> 36 408 18 400 234 NA NA
#> 72 <NA> 37 406 107 397 3632 NA NA
#> 73 <NA> 38 425 25 412 2434 NA NA
#> 74 <NA> 39 449 15 432 342 NA NA
#> 75 <NA> 40 362 7 348 1959 NA NA
#> 76 <NA> 41 381 15 346 1004 NA NA
#> 77 <NA> 42 510 313 488 146 NA NA
#> 78 USA Overall 505 345 485 4888 -32 -8.8
#> 79 <NA> 1 479 50 475 1219 NA NA
#> 80 <NA> 2 490 16 448 1323 NA NA
#> 81 <NA> 3 502 34 488 462 NA NA
#> 82 <NA> 4 528 42 507 263 NA NA
#> 83 <NA> 5 512 42 503 335 NA NA
#> 84 <NA> 6 520 21 477 526 NA NA
#> 85 <NA> 7 565 80 559 278 NA NA
#> 86 <NA> 8 560 41 541 207 NA NA
#> 87 <NA> 9 511 14 529 259 NA NA
#> 88 <NA> 10 522 5 461 16 NA NAThe plot function creates the multilevel assessment
plot. Here it is depicted with side panels showing the distribution of
math scores for all strata for public school students to the left and
private school students below. These panels can be plotted separately
using the mlpsa.circ.plot and mlpsa.distribution.plot
functions.
plot(results.psa.math)
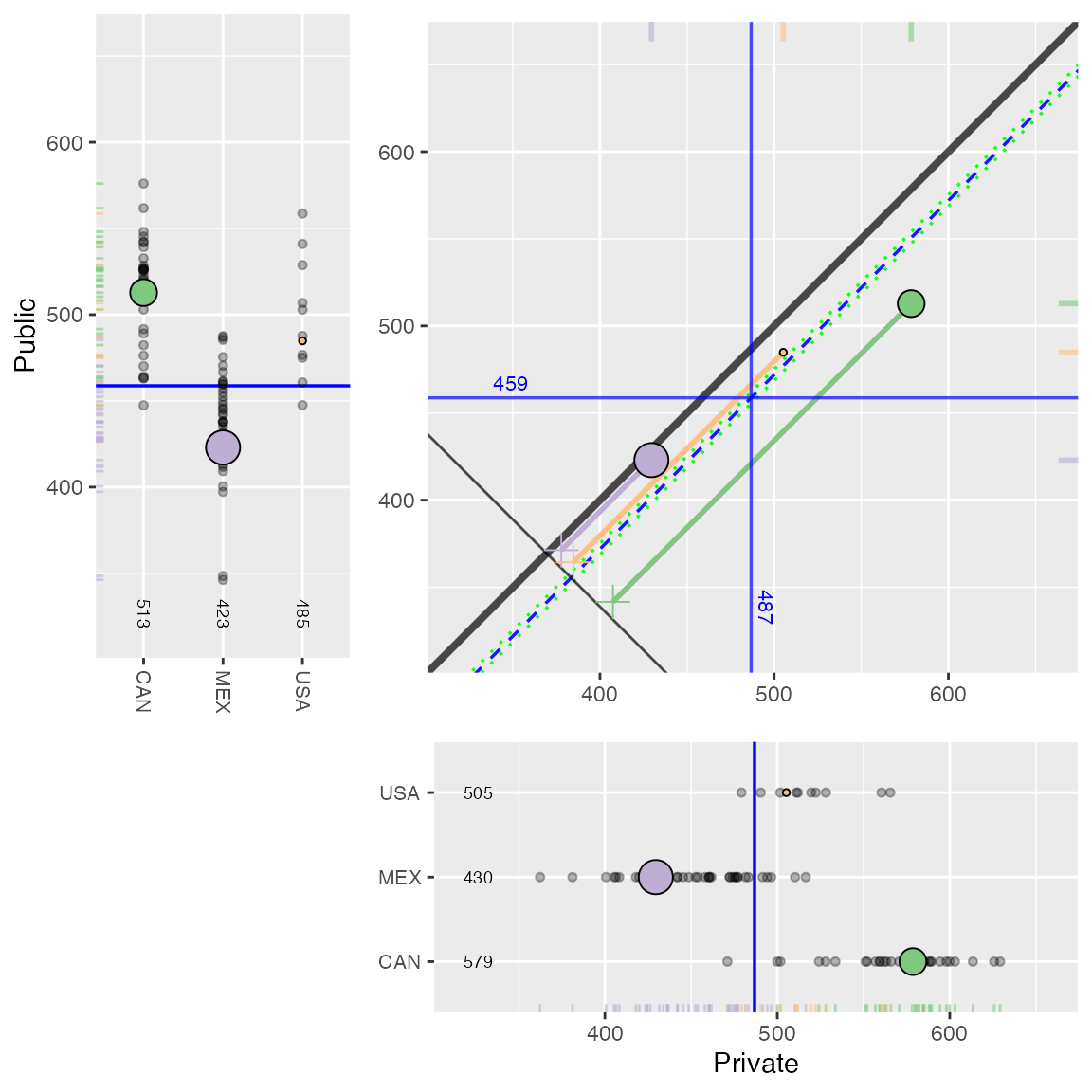
Multilevel PSA assessment plot for PISA. The main panel provides the adjusted mean for private (x-axis) and public (y-axis) for each country. The left and lower panels provide the mean for each stratum for the public and private students, respectively. The overall adjusted mean difference is represented by the dashed blue line and the 95% confidence interval by the dashed green lines. There is a statistically significant difference between private and public school student performance as evidenced by the confidence interval not spanning zero (i.e. not crossing the unit line y=x.
Lastly, the mlpsa.difference.plot function plots the
overall differences. The sd parameter is optional, but if
specified, the x-axis can be interpreted as standardized effect
sizes.
mlpsa.difference.plot(results.psa.math,
sd = mean(mlpsa.df$MathScore, na.rm=TRUE))
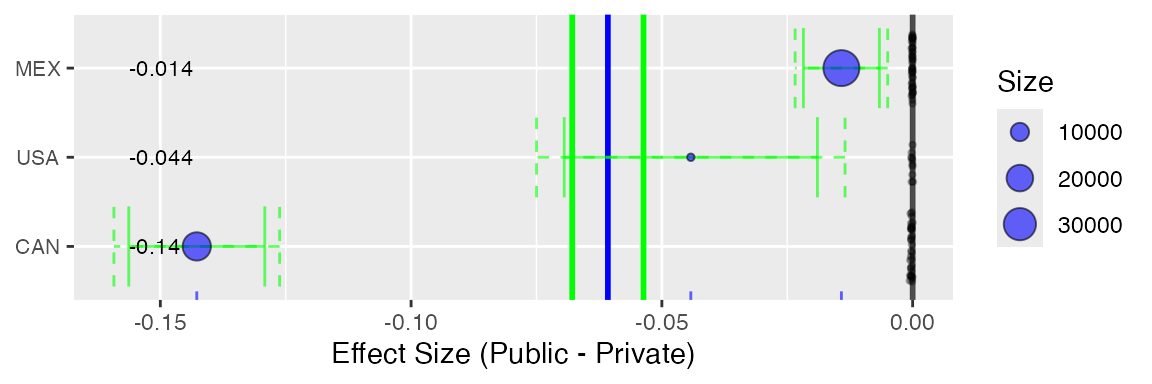
Multilevel PSA difference plot for PISA. Each blue dot corresponds to the effect size (standardized mean difference) for each country. The vertical blue line corresponds to the overall effect size for all countries. The green lines correspond to the 95% confidence intervals. The dashed green lines Bonferroni-Sidak (c.f. Abdi, 2007) adjusted confidence intervals. The size of each dot is proportional to the sample size within each country.