Supports Multiple Methods for Defining and Visualizing (PS) Strata
Source:R/cstrata.psa.R
cstrata.psa.RdGiven propensity scores, allows strata to be directly user defined, possibly to: equalize sizes of strata, equalize the ranges of propensity scores, or to specify cut points on the unit interval. Once strata are created, a simple graphic is generated to visualize or judge strata for overlap and appropriateness. If a regression tree has been used, propensity scores are defined for each leaf of the tree.
Arguments
- treatment
Binary vector or factor defining the two treatments
- propensity
Vector of same length as
treatmentcontaining estimated propensity scores.- strata
Either a vector of same length as
treatmentof predefined stratum number, or one integernused to assign rows tonstratapropensityscores, each of approximately the same number of cases. If relatively few unique propensity scores have been defined (as from a classification tree) then the logicaltreeshould be set equal toTRUE.- int
Either a number
mused to divide[0,1]intomequal length subintervals, or a vector containing cut points between 0 and 1 that define subintervals (perhaps as suggested by loess.psa). In either case the subintervals define strata, for which sizes can differ.- tree
Logical, default
FALSE. If there are few unique propensity scores, say from a recursively partitioned tree, thenTRUEforces strata to be defined by the unique propensity scores.- minsize
Smallest allowable stratum-treatment size. If violated, rows in the stratum are removed. User may wish to redefine strata.
- graphic
Logical, default
TRUE. If set toFALSEthe graphic is not provided.- colors
2-ary color vector. Sets the colors of the points in the graphic. Default =
c("blue", "orange")- xlab
Label for the x axis; default =
"Estimated Propensity Scores with Random Heights".- pch
2-ary vector; determines the shape of points in the graphic. Default =
c(16, 16).
Value
- Original.Strata
Table of strata-treatment sizes before
minsizeevaluation.- Used.Strata
Table of strata-treatment sizes after
minsizeevaluation.- strata
Vector of the same length as
treatment, indicating either the strata input by user or those created by the function.
See also
Examples
data(lindner)
attach(lindner)
#> The following objects are masked from lindner (pos = 3):
#>
#> abcix, acutemi, cardbill, diabetic, ejecfrac, female, height,
#> lifepres, stent, ves1proc
#> The following objects are masked from lindner (pos = 4):
#>
#> abcix, acutemi, cardbill, diabetic, ejecfrac, female, height,
#> lifepres, stent, ves1proc
#> The following objects are masked from lindner (pos = 5):
#>
#> abcix, acutemi, cardbill, diabetic, ejecfrac, female, height,
#> lifepres, stent, ves1proc
lindner.ps <- glm(abcix ~ stent + height + female +
diabetic + acutemi + ejecfrac + ves1proc,
data = lindner, family = binomial)
ps <- lindner.ps$fitted
cstrata.psa(abcix, ps, strata = 5)
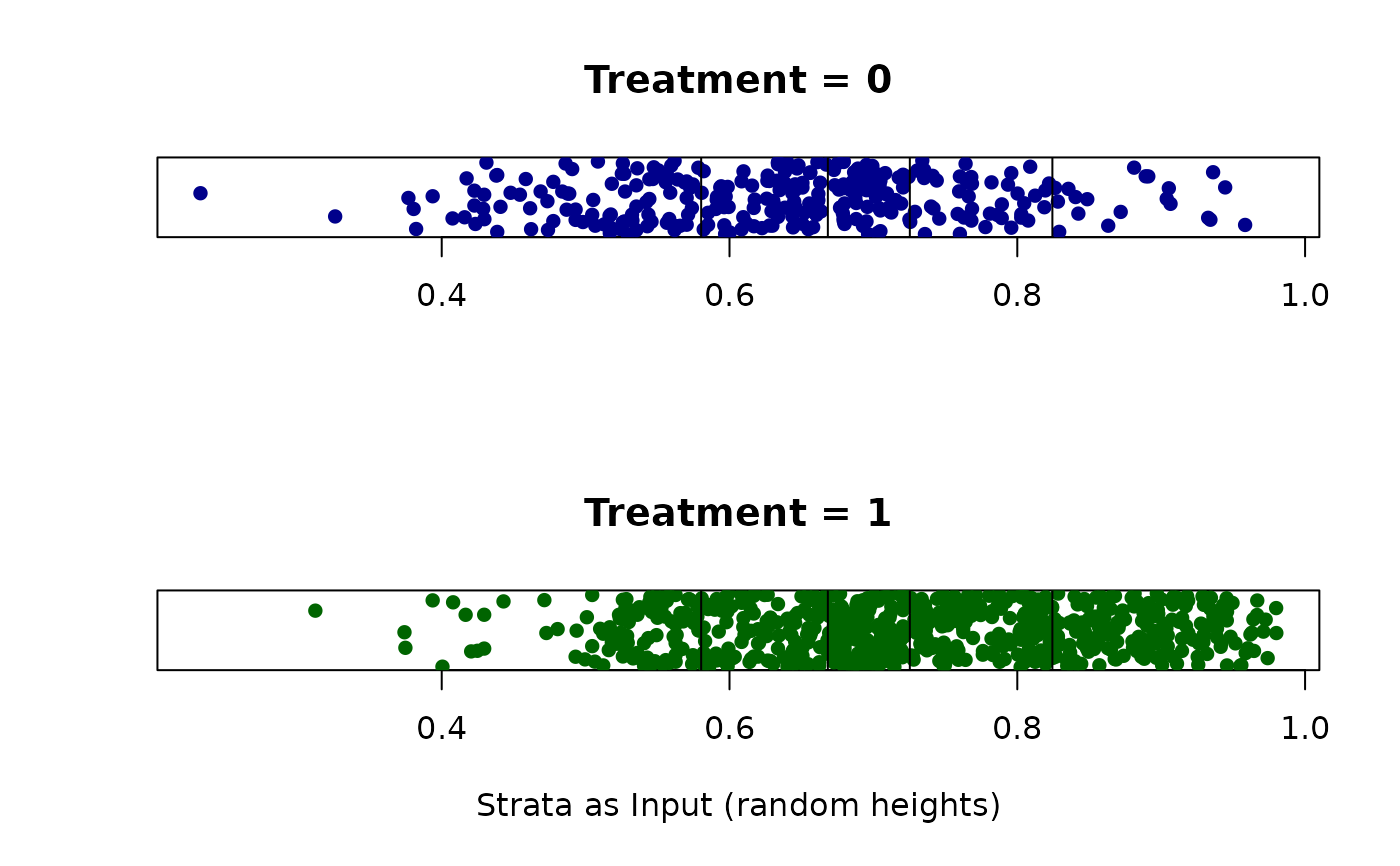 #> $Original.Strata
#> 1 2 3 4 5
#> 0 94 76 64 44 20
#> 1 105 123 134 156 180
#>
#> $Used.Strata
#> 1 2 3 4 5
#> 0 94 76 64 44 20
#> 1 105 123 134 156 180
#> Strata.Size 199 199 198 200 200
#>
#> $strata
#> [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1
#> [38] 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#> [75] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 1 2 2 2
#> [112] 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
#> [149] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
#> [186] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
#> [223] 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [260] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 4
#> [297] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [334] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 4 3 3 3 3 3 3 4 3 3 3 3 3 4 3 3 3 3 3 4 4 4 4
#> [371] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4
#> [408] 4 4 4 4 4 4 4 4 5 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 4 4 4 4 4 4 4 4 4 4 4
#> [445] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4
#> [482] 4 4 4 4 4 4 4 4 4 5 4 5 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4
#> [519] 4 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 4
#> [556] 5 5 5 5 5 5 5 5 5 4 5 5 5 5 5 5 5 5 5 5 5 5 5 4 5 5 5 5 5 5 5 5 5 5 5 5 5
#> [593] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5
#> [630] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5
#> [667] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 1 1 1 1 1
#> [704] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#> [741] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#> [778] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
#> [815] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
#> [852] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 2 3 3 3 3 3 3 3 3
#> [889] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [926] 3 3 3 3 3 4 4 4 3 4 4 4 4 4 4 4 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4
#> [963] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5
#>
cstrata.psa(abcix, ps, strata = 10)
#> $Original.Strata
#> 1 2 3 4 5
#> 0 94 76 64 44 20
#> 1 105 123 134 156 180
#>
#> $Used.Strata
#> 1 2 3 4 5
#> 0 94 76 64 44 20
#> 1 105 123 134 156 180
#> Strata.Size 199 199 198 200 200
#>
#> $strata
#> [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1
#> [38] 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#> [75] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 1 2 2 2
#> [112] 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
#> [149] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
#> [186] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
#> [223] 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [260] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 4
#> [297] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [334] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 4 3 3 3 3 3 3 4 3 3 3 3 3 4 3 3 3 3 3 4 4 4 4
#> [371] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4
#> [408] 4 4 4 4 4 4 4 4 5 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 4 4 4 4 4 4 4 4 4 4 4
#> [445] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4
#> [482] 4 4 4 4 4 4 4 4 4 5 4 5 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4
#> [519] 4 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 4
#> [556] 5 5 5 5 5 5 5 5 5 4 5 5 5 5 5 5 5 5 5 5 5 5 5 4 5 5 5 5 5 5 5 5 5 5 5 5 5
#> [593] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5
#> [630] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5
#> [667] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 1 1 1 1 1
#> [704] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#> [741] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#> [778] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
#> [815] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
#> [852] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 2 3 3 3 3 3 3 3 3
#> [889] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [926] 3 3 3 3 3 4 4 4 3 4 4 4 4 4 4 4 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4
#> [963] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5
#>
cstrata.psa(abcix, ps, strata = 10)
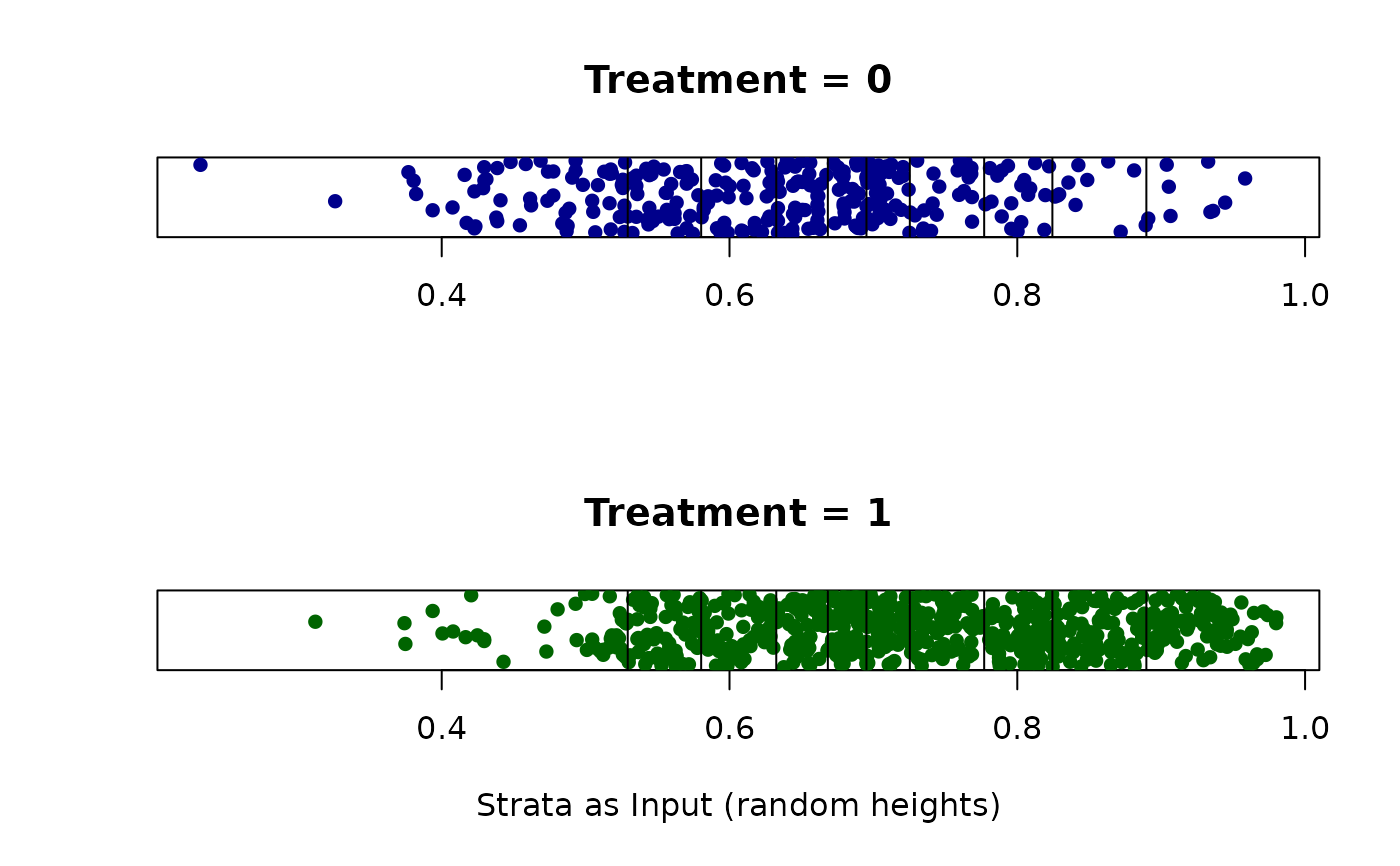 #> $Original.Strata
#> 1 2 3 4 5 6 7 8 9 10
#> 0 58 36 36 40 29 35 25 19 11 9
#> 1 42 63 64 59 71 63 76 80 89 91
#>
#> $Used.Strata
#> 1 2 3 4 5 6 7 8 9 10
#> 0 58 36 36 40 29 35 25 19 11 9
#> 1 42 63 64 59 71 63 76 80 89 91
#> Strata.Size 100 99 100 99 100 98 101 99 100 100
#>
#> $strata
#> [1] 1 2 1 1 1 2 1 2 2 1 2 2 1 1 2 2 2 2 1 1 1 1 2 2 1
#> [26] 2 2 1 2 1 2 2 2 1 3 1 2 1 3 2 1 1 1 1 2 1 2 2 2 1
#> [51] 2 1 2 1 2 2 1 2 1 1 1 2 2 2 2 1 2 2 1 1 2 1 2 2 2
#> [76] 2 2 2 1 1 2 1 2 2 2 2 2 2 1 2 2 2 1 2 2 2 2 1 2 1
#> [101] 2 1 2 2 2 3 3 2 4 3 4 3 3 4 4 4 3 4 2 3 3 4 4 3 3
#> [126] 3 3 3 3 4 4 4 4 4 3 4 3 3 3 3 4 4 3 3 3 4 4 3 4 4
#> [151] 3 4 3 4 3 4 4 4 4 4 3 3 4 4 3 4 3 3 3 4 4 4 4 4 4
#> [176] 3 4 3 3 4 3 4 4 3 3 4 3 4 3 4 3 3 4 3 4 3 3 3 4 4
#> [201] 4 3 4 3 3 5 3 4 3 4 3 3 3 4 3 4 4 3 4 4 3 3 3 3 3
#> [226] 4 3 4 4 5 5 5 5 5 5 6 6 6 5 6 5 5 6 5 5 5 5 6 5 5
#> [251] 6 5 6 6 5 5 5 5 6 5 5 5 6 6 6 6 5 5 6 6 6 6 6 5 6
#> [276] 5 5 6 6 5 6 6 5 6 5 5 5 5 6 6 5 5 6 6 5 7 6 5 5 5
#> [301] 6 5 5 6 5 5 6 6 5 6 5 6 6 5 5 6 6 5 5 5 6 5 5 5 6
#> [326] 5 5 6 6 5 5 6 6 5 5 6 6 5 6 6 6 5 6 6 6 6 6 7 6 6
#> [351] 6 5 5 6 7 5 6 5 5 6 7 5 5 6 5 6 7 7 7 8 8 7 7 8 7
#> [376] 8 7 7 7 7 8 8 8 8 8 8 7 7 7 7 8 7 8 7 7 7 8 8 8 7
#> [401] 8 7 8 8 8 7 7 7 8 8 7 8 7 8 7 9 7 8 7 7 8 7 8 8 7
#> [426] 7 7 7 8 7 7 7 9 8 7 7 7 7 8 8 7 8 7 8 8 8 8 8 7 7
#> [451] 8 8 8 7 7 7 8 8 7 7 7 7 8 8 8 7 8 8 8 8 8 8 7 7 8
#> [476] 7 8 8 7 8 8 8 8 8 8 7 7 8 8 8 9 7 9 8 8 7 8 7 7 8
#> [501] 7 7 7 8 8 8 7 8 8 8 8 7 7 8 8 8 7 7 7 10 9 9 9 10 10
#> [526] 9 9 9 9 10 10 10 10 10 9 9 10 10 9 9 9 9 9 9 10 9 9 9 10 9
#> [551] 10 10 9 9 8 10 10 9 9 10 9 9 10 9 8 9 10 10 9 9 9 9 9 9 9
#> [576] 9 9 10 8 10 9 10 10 10 10 9 9 10 10 10 10 9 10 10 10 9 10 10 10 9
#> [601] 9 10 9 10 9 9 10 9 9 9 9 9 10 10 9 10 10 9 9 10 10 9 10 9 9
#> [626] 9 9 10 9 10 10 10 10 10 10 10 10 10 10 9 9 9 10 10 9 10 10 10 10 9
#> [651] 10 9 10 9 10 9 9 10 10 9 10 10 9 9 10 9 10 10 10 9 9 10 10 9 10
#> [676] 9 10 9 10 10 10 10 10 9 9 10 10 9 9 10 9 10 10 10 9 9 10 10 1 1
#> [701] 2 1 1 1 1 2 1 2 1 1 1 1 2 1 1 1 1 2 1 1 2 1 1 1 1
#> [726] 2 2 1 1 1 2 1 2 2 2 1 2 1 1 1 1 2 2 1 1 2 1 1 2 1
#> [751] 2 1 2 1 1 2 2 2 2 2 2 2 1 1 1 2 1 1 1 1 1 1 1 1 2
#> [776] 2 2 2 2 1 1 2 1 1 1 2 1 1 1 2 2 1 4 3 3 3 4 4 3 3
#> [801] 4 3 3 4 3 3 3 4 4 3 4 4 4 4 4 4 3 4 4 3 4 4 4 4 3
#> [826] 4 4 4 3 4 3 4 3 4 3 4 4 3 4 3 4 3 4 4 3 3 3 3 3 4
#> [851] 4 3 3 4 3 3 4 4 4 3 4 3 3 4 3 3 3 6 6 6 6 6 5 6 6
#> [876] 5 6 5 6 4 5 6 5 6 5 6 6 5 6 5 5 5 6 6 6 5 5 6 5 5
#> [901] 6 5 6 5 5 5 6 6 6 6 5 5 6 6 5 5 5 5 6 6 5 6 6 5 5
#> [926] 6 5 6 6 5 8 8 7 6 8 8 8 7 7 8 7 6 7 7 7 8 7 7 8 8
#> [951] 8 7 7 8 7 8 8 7 7 8 7 8 7 8 7 8 7 7 7 7 7 8 7 7 8
#> [976] 7 9 10 10 10 9 9 9 10 9 9 9 10 9 10 10 9 10 9 10 9
#>
cstrata.psa(abcix, ps, int = c(.37, .56, .87, 1))
#> $Original.Strata
#> 1 2 3 4 5 6 7 8 9 10
#> 0 58 36 36 40 29 35 25 19 11 9
#> 1 42 63 64 59 71 63 76 80 89 91
#>
#> $Used.Strata
#> 1 2 3 4 5 6 7 8 9 10
#> 0 58 36 36 40 29 35 25 19 11 9
#> 1 42 63 64 59 71 63 76 80 89 91
#> Strata.Size 100 99 100 99 100 98 101 99 100 100
#>
#> $strata
#> [1] 1 2 1 1 1 2 1 2 2 1 2 2 1 1 2 2 2 2 1 1 1 1 2 2 1
#> [26] 2 2 1 2 1 2 2 2 1 3 1 2 1 3 2 1 1 1 1 2 1 2 2 2 1
#> [51] 2 1 2 1 2 2 1 2 1 1 1 2 2 2 2 1 2 2 1 1 2 1 2 2 2
#> [76] 2 2 2 1 1 2 1 2 2 2 2 2 2 1 2 2 2 1 2 2 2 2 1 2 1
#> [101] 2 1 2 2 2 3 3 2 4 3 4 3 3 4 4 4 3 4 2 3 3 4 4 3 3
#> [126] 3 3 3 3 4 4 4 4 4 3 4 3 3 3 3 4 4 3 3 3 4 4 3 4 4
#> [151] 3 4 3 4 3 4 4 4 4 4 3 3 4 4 3 4 3 3 3 4 4 4 4 4 4
#> [176] 3 4 3 3 4 3 4 4 3 3 4 3 4 3 4 3 3 4 3 4 3 3 3 4 4
#> [201] 4 3 4 3 3 5 3 4 3 4 3 3 3 4 3 4 4 3 4 4 3 3 3 3 3
#> [226] 4 3 4 4 5 5 5 5 5 5 6 6 6 5 6 5 5 6 5 5 5 5 6 5 5
#> [251] 6 5 6 6 5 5 5 5 6 5 5 5 6 6 6 6 5 5 6 6 6 6 6 5 6
#> [276] 5 5 6 6 5 6 6 5 6 5 5 5 5 6 6 5 5 6 6 5 7 6 5 5 5
#> [301] 6 5 5 6 5 5 6 6 5 6 5 6 6 5 5 6 6 5 5 5 6 5 5 5 6
#> [326] 5 5 6 6 5 5 6 6 5 5 6 6 5 6 6 6 5 6 6 6 6 6 7 6 6
#> [351] 6 5 5 6 7 5 6 5 5 6 7 5 5 6 5 6 7 7 7 8 8 7 7 8 7
#> [376] 8 7 7 7 7 8 8 8 8 8 8 7 7 7 7 8 7 8 7 7 7 8 8 8 7
#> [401] 8 7 8 8 8 7 7 7 8 8 7 8 7 8 7 9 7 8 7 7 8 7 8 8 7
#> [426] 7 7 7 8 7 7 7 9 8 7 7 7 7 8 8 7 8 7 8 8 8 8 8 7 7
#> [451] 8 8 8 7 7 7 8 8 7 7 7 7 8 8 8 7 8 8 8 8 8 8 7 7 8
#> [476] 7 8 8 7 8 8 8 8 8 8 7 7 8 8 8 9 7 9 8 8 7 8 7 7 8
#> [501] 7 7 7 8 8 8 7 8 8 8 8 7 7 8 8 8 7 7 7 10 9 9 9 10 10
#> [526] 9 9 9 9 10 10 10 10 10 9 9 10 10 9 9 9 9 9 9 10 9 9 9 10 9
#> [551] 10 10 9 9 8 10 10 9 9 10 9 9 10 9 8 9 10 10 9 9 9 9 9 9 9
#> [576] 9 9 10 8 10 9 10 10 10 10 9 9 10 10 10 10 9 10 10 10 9 10 10 10 9
#> [601] 9 10 9 10 9 9 10 9 9 9 9 9 10 10 9 10 10 9 9 10 10 9 10 9 9
#> [626] 9 9 10 9 10 10 10 10 10 10 10 10 10 10 9 9 9 10 10 9 10 10 10 10 9
#> [651] 10 9 10 9 10 9 9 10 10 9 10 10 9 9 10 9 10 10 10 9 9 10 10 9 10
#> [676] 9 10 9 10 10 10 10 10 9 9 10 10 9 9 10 9 10 10 10 9 9 10 10 1 1
#> [701] 2 1 1 1 1 2 1 2 1 1 1 1 2 1 1 1 1 2 1 1 2 1 1 1 1
#> [726] 2 2 1 1 1 2 1 2 2 2 1 2 1 1 1 1 2 2 1 1 2 1 1 2 1
#> [751] 2 1 2 1 1 2 2 2 2 2 2 2 1 1 1 2 1 1 1 1 1 1 1 1 2
#> [776] 2 2 2 2 1 1 2 1 1 1 2 1 1 1 2 2 1 4 3 3 3 4 4 3 3
#> [801] 4 3 3 4 3 3 3 4 4 3 4 4 4 4 4 4 3 4 4 3 4 4 4 4 3
#> [826] 4 4 4 3 4 3 4 3 4 3 4 4 3 4 3 4 3 4 4 3 3 3 3 3 4
#> [851] 4 3 3 4 3 3 4 4 4 3 4 3 3 4 3 3 3 6 6 6 6 6 5 6 6
#> [876] 5 6 5 6 4 5 6 5 6 5 6 6 5 6 5 5 5 6 6 6 5 5 6 5 5
#> [901] 6 5 6 5 5 5 6 6 6 6 5 5 6 6 5 5 5 5 6 6 5 6 6 5 5
#> [926] 6 5 6 6 5 8 8 7 6 8 8 8 7 7 8 7 6 7 7 7 8 7 7 8 8
#> [951] 8 7 7 8 7 8 8 7 7 8 7 8 7 8 7 8 7 7 7 7 7 8 7 7 8
#> [976] 7 9 10 10 10 9 9 9 10 9 9 9 10 9 10 10 9 10 9 10 9
#>
cstrata.psa(abcix, ps, int = c(.37, .56, .87, 1))
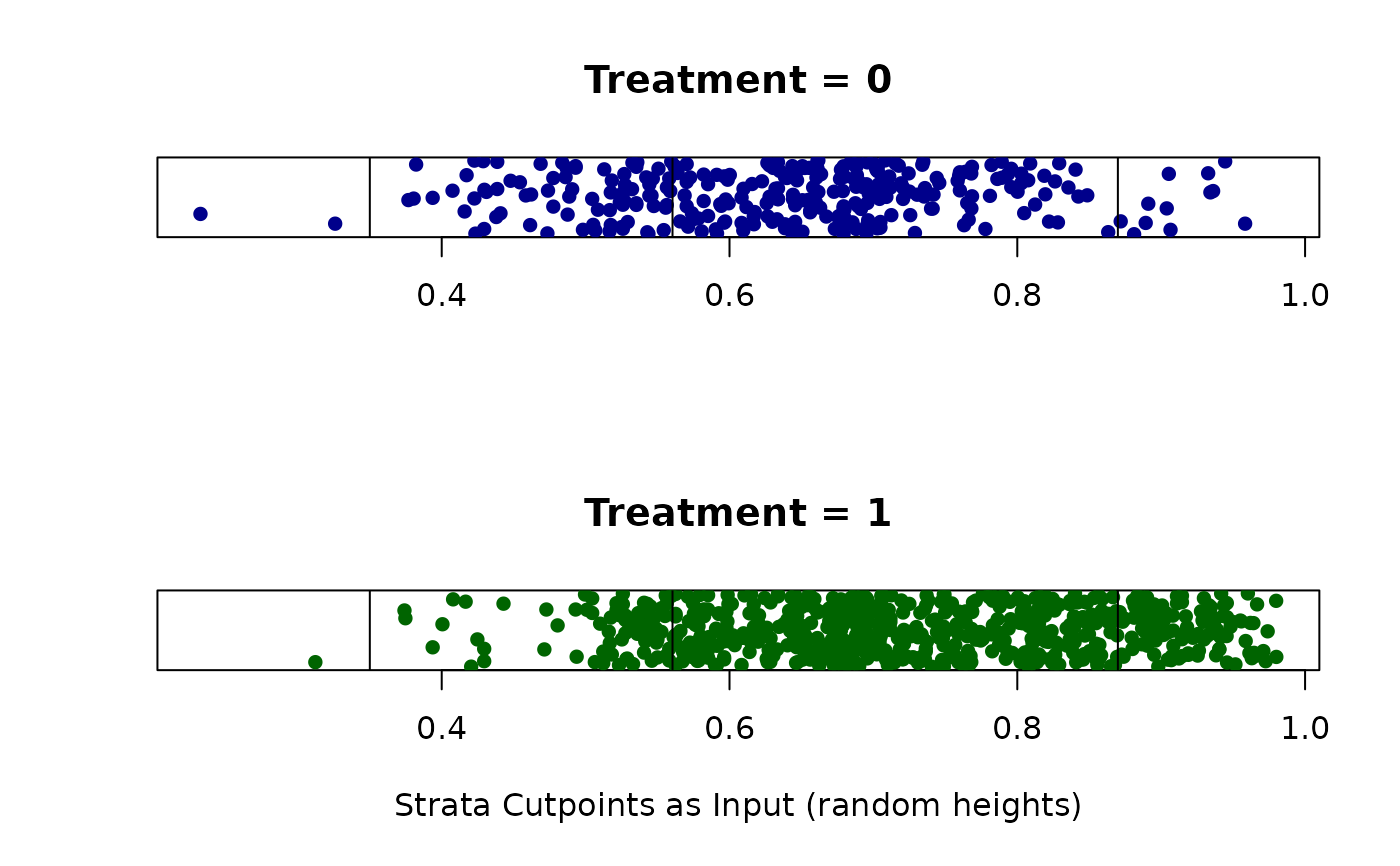 #> $Original.Strata
#> 1 2 3 4
#> 0 2 78 206 12
#> 1 1 77 507 113
#>
#> $Used.Strata
#> 2 3 4
#> 0 78 206 12
#> 1 77 507 113
#> Strata.Size 155 713 125
#>
#> $strata
#> [1] 2 3 2 2 2 3 2 3 2 2 2 3 2 2 2 3 2 2 2 2 2 1 3 3 2 2 2 2 2 2 3 2 2 2 3 2 2
#> [38] 2 3 2 2 2 2 2 2 2 2 2 3 2 2 2 3 2 2 2 2 2 2 2 2 2 2 3 2 2 3 3 2 2 3 2 2 2
#> [75] 2 3 2 3 2 2 2 2 3 2 3 2 3 3 2 2 3 3 2 2 2 2 3 2 2 2 2 2 3 3 2 3 3 3 3 3 3
#> [112] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [149] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [186] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [223] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [260] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [297] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [334] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [371] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [408] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [445] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [482] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [519] 3 4 4 3 3 4 4 3 3 3 3 4 4 4 4 4 3 3 4 4 3 4 3 3 3 4 4 4 4 3 4 3 4 4 3 3 3
#> [556] 4 4 4 3 4 4 4 4 3 3 3 4 4 4 3 4 3 3 3 3 3 3 4 3 4 3 4 4 4 4 3 3 4 4 4 4 3
#> [593] 4 4 4 3 4 4 4 3 4 4 4 4 4 3 4 4 3 3 3 3 4 4 4 4 4 3 3 4 4 3 4 3 4 3 4 4 3
#> [630] 4 4 4 4 4 4 4 4 4 4 4 4 3 4 4 3 4 4 4 4 3 4 3 4 4 4 3 3 4 4 3 4 4 4 3 4 3
#> [667] 4 4 4 3 3 4 4 3 4 3 4 3 4 4 4 4 4 3 4 4 4 3 3 4 3 4 4 4 3 3 4 4 2 2 3 2 2
#> [704] 2 2 2 2 3 2 2 2 2 3 2 2 1 2 2 2 2 3 2 2 2 2 2 2 2 2 2 3 2 3 2 3 2 2 2 2 2
#> [741] 2 3 2 2 2 2 2 1 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3 2
#> [778] 2 3 2 2 2 2 2 2 3 2 2 2 2 3 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [815] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [852] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [889] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [926] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [963] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 3 4 3 4 3 3 3 4 3 4 4 3 4 4 4 3
#>
#> $Original.Strata
#> 1 2 3 4
#> 0 2 78 206 12
#> 1 1 77 507 113
#>
#> $Used.Strata
#> 2 3 4
#> 0 78 206 12
#> 1 77 507 113
#> Strata.Size 155 713 125
#>
#> $strata
#> [1] 2 3 2 2 2 3 2 3 2 2 2 3 2 2 2 3 2 2 2 2 2 1 3 3 2 2 2 2 2 2 3 2 2 2 3 2 2
#> [38] 2 3 2 2 2 2 2 2 2 2 2 3 2 2 2 3 2 2 2 2 2 2 2 2 2 2 3 2 2 3 3 2 2 3 2 2 2
#> [75] 2 3 2 3 2 2 2 2 3 2 3 2 3 3 2 2 3 3 2 2 2 2 3 2 2 2 2 2 3 3 2 3 3 3 3 3 3
#> [112] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [149] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [186] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [223] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [260] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [297] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [334] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [371] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [408] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [445] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [482] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [519] 3 4 4 3 3 4 4 3 3 3 3 4 4 4 4 4 3 3 4 4 3 4 3 3 3 4 4 4 4 3 4 3 4 4 3 3 3
#> [556] 4 4 4 3 4 4 4 4 3 3 3 4 4 4 3 4 3 3 3 3 3 3 4 3 4 3 4 4 4 4 3 3 4 4 4 4 3
#> [593] 4 4 4 3 4 4 4 3 4 4 4 4 4 3 4 4 3 3 3 3 4 4 4 4 4 3 3 4 4 3 4 3 4 3 4 4 3
#> [630] 4 4 4 4 4 4 4 4 4 4 4 4 3 4 4 3 4 4 4 4 3 4 3 4 4 4 3 3 4 4 3 4 4 4 3 4 3
#> [667] 4 4 4 3 3 4 4 3 4 3 4 3 4 4 4 4 4 3 4 4 4 3 3 4 3 4 4 4 3 3 4 4 2 2 3 2 2
#> [704] 2 2 2 2 3 2 2 2 2 3 2 2 1 2 2 2 2 3 2 2 2 2 2 2 2 2 2 3 2 3 2 3 2 2 2 2 2
#> [741] 2 3 2 2 2 2 2 1 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3 2
#> [778] 2 3 2 2 2 2 2 2 3 2 2 2 2 3 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [815] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [852] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [889] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [926] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [963] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 3 4 3 4 3 3 3 4 3 4 4 3 4 4 4 3
#>