medley: Predictive Modeling with Missing Data
Jason Bryer, Ph.D.
Source:vignettes/medley.Rmd
medley.RmdIntroduction
Most predictive modeling strategies require complete data to train
and predict outcomes. A common strategy is to impute the missing data
before training the models. However, in many situations, missing data
occurs in a systematic way therefore violating the missing completely at
random (MCAR) assumption. For instance, data may be collected over
multiple time periods or the available data may vary depending on
varying collection protocols or selection bias at the individual level.
The medley package provides a framework for estimating
predictive model that takes into account the patterns of missing
data.
The motivating example for this approach predictive modeling comes from predicting student success in college. Institutions have become increasingly interested in using predictive models to identify students at risk for attrition as early as possible in order to provided targeted interventions and supports. Information about students is collected over several months beginning at the college application phase, commitment to enroll, orientation, and finally behavior data as the student begins coursework. In addition to missing data being related to where the student is in the process, students may opt to not provide certain data elements. This results in a complex system where a single predictive model is appropriate.
Data Source
This paper will explore data from the Diagnostic Assessment and
Achievement of College Skills (DAACS; https://daacs.net). DAACS is a suite of technological
and social supports designed to optimize student learning. Students
complete assessments in self-regulated learning, writing, mathematics,
and reading and upon completion receive immediate feedback in terms of
developing, emerging, and mastering. The feedback is tailored to their
results. The data for this paper was part of a larger randomized control
trial where DAACS was embedded within orientation for the treatment
students. Although students were instructed that orientation was
required, there were no consequences for not completing orientation and
therefore approximately 43% of students did not attempt orientation, and
therefore did not complete DAACS. The goal is to predicted term-to-term
retention (the retained variable) for each student based
upon the available data. Table @ref(tab:descriptives) for descriptive
statistics which reveals that the DAACS results are not complete for
some students. The overall retention rate is 56.17%.
| Variable | N | Mean | Std Dev | Median |
|---|---|---|---|---|
| retained | 5154 | |||
| … No | 2259 | 44% | ||
| … Yes | 2895 | 56% | ||
| page_views | 39 | 24 | 34 | |
| srl | 2.8 | 0.43 | 2.8 | |
| math | 0.58 | 0.2 | 0.61 | |
| reading | 0.85 | 0.17 | 0.89 | |
| writing | 0.78 | 0.16 | 0.83 | |
| income | 4.4 | 2.4 | 4 | |
| employment | 2.6 | 0.75 | 3 | |
| ell | 0.93 | 0.26 | 1 | |
| ed_mother | 3.3 | 2 | 3 | |
| ed_father | 3.2 | 2 | 3 | |
| ethnicity | 5154 | |||
| … Black or African American | 1049 | 20% | ||
| … Hispanic | 699 | 14% | ||
| … Other | 548 | 11% | ||
| … White | 2858 | 55% | ||
| gender | 5154 | |||
| … FEMALE | 2123 | 41% | ||
| … MALE | 3031 | 59% | ||
| military | 5154 | |||
| … No | 2881 | 56% | ||
| … Yes | 2273 | 44% | ||
| age | 35 | 9.3 | 34 |
Missing Data Patterns
To begin we first explore the patterns of missing data. Figure @ref(fig:upset) is an UpSet plot (Gu, Eils, and Schlesner 2016) created from a shadow matrix1. Each vertical line corresponds to a set, or combination, of variables. The dots indicate that that variable is included in the set. The bars on the top correspond to the number of observations in that set and the bars to the right correspond to the total number of observed values. The largest set includes only the demographics variables, the second largest included demographics and all DAACS variables. There is a third set that includes self-regulated learning along with demographics that is worth considering since it contains more than 10% of the observations. It should be noted that there is a potential fourth set which included demographic variables along with three of DAACS variables (SRL, reading, and math). However, since this set has fewer than 10% of the observations we will use a three set/model solution.
shadow_matrix <- as.data.frame(!is.na(daacs))
ComplexHeatmap::make_comb_mat(shadow_matrix) |> ComplexHeatmap::UpSet(right_annotation = NULL)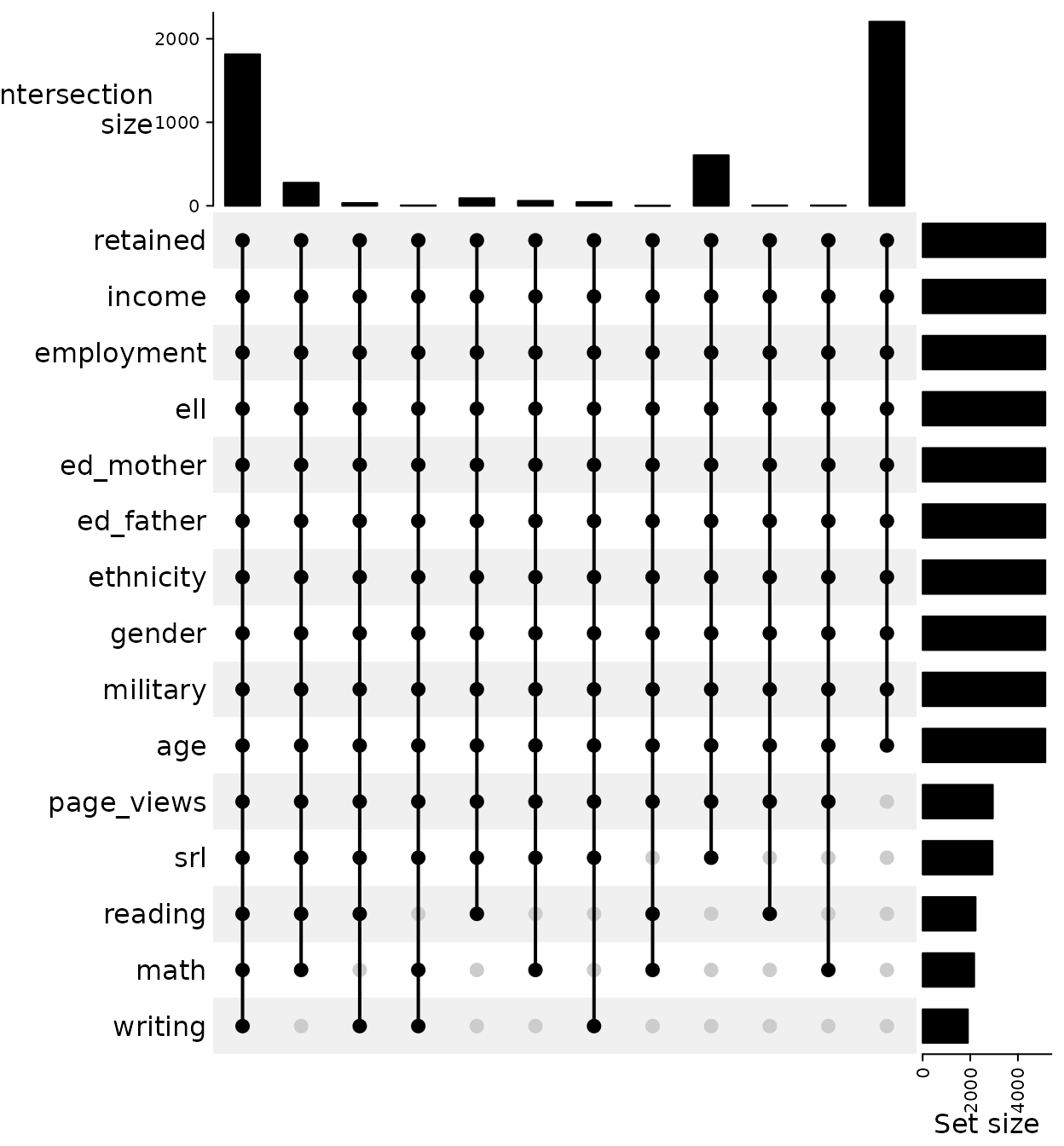
UpSet plot of the missing data
Baseline Models
There are generally two choices when estimating models when there is missing data: 1) Model using only the available data or 2) Impute the missing data before modeling.
Using available data
In the DAACS data set as depicted in Figure @ref(fig:upset) the demographics variables were observed for all students. To start we train a logistic regression model on the training data.
lr_out <- glm(data = daacs_train,
formula = retained ~ income + employment + ell + ed_mother + ed_father +
ethnicity + gender + military + age,
family = binomial(link = 'logit'))
rf_out <- randomForest(formula = factor(retained) ~ income + employment + ell + ed_mother + ed_father +
ethnicity + gender + military + age,
data = daacs_train)We can get predicted values from the validation data set and print the confusion matrix.
lr_predictions <- predict(lr_out, newdata = daacs_valid, type = 'response')
confusion_matrix(observed = daacs_valid$retained,
predicted = lr_predictions > 0.5)
#> predicted
#> observed FALSE TRUE
#> FALSE 295 (19.07%) 386 (24.95%)
#> TRUE 216 (13.96%) 650 (42.02%)
#> Accuracy: 61.09%
#> Sensitivity: 43.32%
#> Specificity: 75.06%
rf_predictions <- predict(rf_out, newdata = daacs_valid, type = 'response')
confusion_matrix(observed = daacs_valid$retained,
predicted = rf_predictions)
#> predicted
#> observed FALSE TRUE
#> FALSE 279 (18.03%) 402 (25.99%)
#> TRUE 251 (16.22%) 615 (39.75%)
#> Accuracy: 57.79%
#> Sensitivity: 40.97%
#> Specificity: 71.02%The overall accuracy using only the demographic variables is 61.09%
Note that for random forests we used type = 'response'
which provides the predicted class. If you wish to get predicted
probabilities instead use type = 'prob' (also random forest
returns a two column of predicted values, column 2 corresponds to the
predicted probability of the “success” class). This is useful if you
wish to plot a receiver operating characteristic (ROC) curve as shown in
the figure below.
calculate_roc(
predictions = predict(rf_out, newdata = daacs_valid, type = 'prob')[,2],
observed = daacs_valid$retained
) |> plot()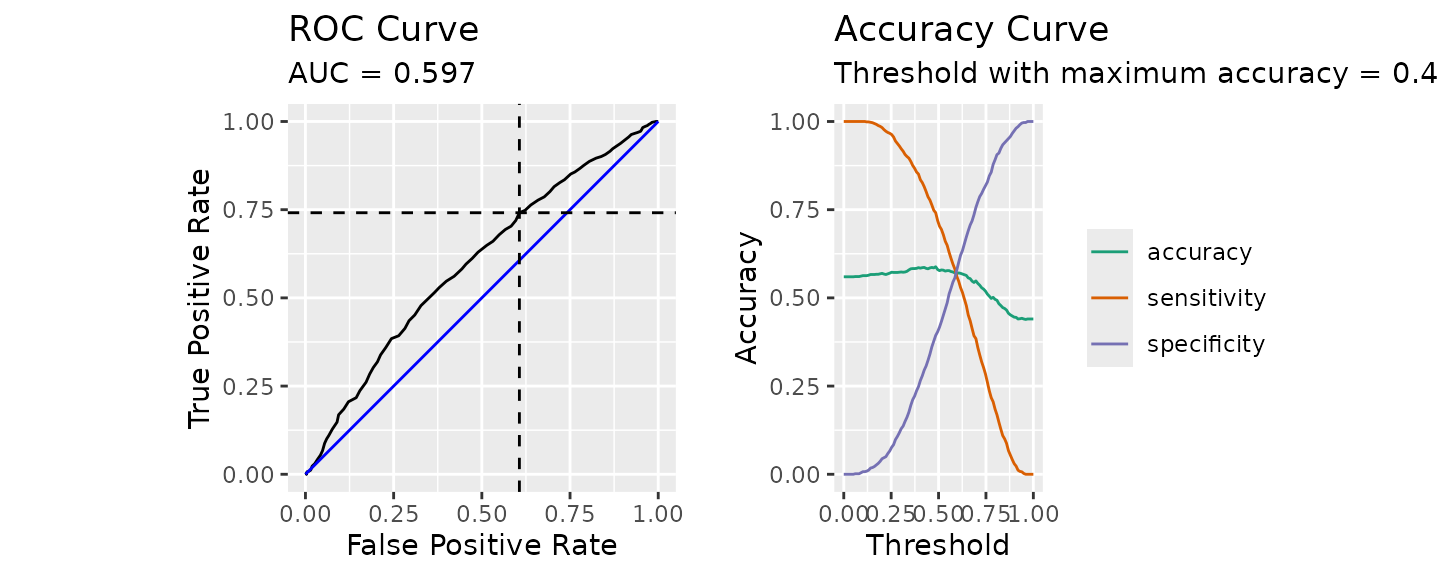
Mean Imputation
daacs_complete_mean <- daacs
for(i in 2:ncol(daacs_complete_mean)) {
missing_rows <- is.na(daacs_complete_mean[,i])
if(sum(missing_rows) > 0) {
daacs_complete_mean[missing_rows, i] <- mean(daacs_complete_mean[,i], na.rm = TRUE)
}
}
daacs_train_complete_mean <- daacs_complete_mean[train_rows,]
daacs_valid_complete_mean <- daacs_complete_mean[-train_rows,]
mean_lr_out <- glm(formula = retained ~ .,
data = daacs_train_complete_mean,
family = binomial(link = logit))
mean_lr_predictions <- predict(mean_lr_out, newdata = daacs_valid_complete_mean, type = 'response')
confusion_matrix(observed = daacs_valid_complete_mean$retained,
predicted = mean_lr_predictions > 0.5)
#> predicted
#> observed FALSE TRUE
#> FALSE 292 (18.88%) 389 (25.15%)
#> TRUE 212 (13.70%) 654 (42.28%)
#> Accuracy: 61.15%
#> Sensitivity: 42.88%
#> Specificity: 75.52%
mean_rf_out <- randomForest(formula = factor(retained) ~ .,
data = daacs_train_complete_mean)
mean_rf_predictions <- predict(mean_rf_out, newdata = daacs_valid_complete_mean, type = 'response')
confusion_matrix(observed = daacs_valid_complete_mean$retained,
predicted = mean_rf_predictions)
#> predicted
#> observed FALSE TRUE
#> FALSE 316 (20.43%) 365 (23.59%)
#> TRUE 178 (11.51%) 688 (44.47%)
#> Accuracy: 64.9%
#> Sensitivity: 46.4%
#> Specificity: 79.45%Multiple imputation
Another common approach to modeling with missing data is multiple
imputation. The mice package (Multivariate Imputations by
Chained Equations) is a robust and popular approach to imputing missing
data. For simplicity we will use the final imputed data set for
comparison2.
mice_out <- mice::mice(daacs[,-1], M = 5, seed = 2112, printFlag = FALSE)
daacs_complete_mice <- cbind(retained = daacs$retained, mice::complete(mice_out))
daacs_train_complete_mice <- daacs_complete_mice[train_rows,]
daacs_valid_complete_mice <- daacs_complete_mice[-train_rows,]With the missing DAACS data imputed we can train a logistic regression model using the full data set.
mice_lr_out <- glm(formula = retained ~ .,
data = daacs_train_complete_mice,
family = binomial(link = logit))
mice_lr_predictions <- predict(mice_lr_out, newdata = daacs_valid_complete_mice, type = 'response')
confusion_matrix(observed = daacs_valid_complete_mice$retained,
predicted = mice_lr_predictions > 0.5)
#> predicted
#> observed FALSE TRUE
#> FALSE 297 (19.20%) 384 (24.82%)
#> TRUE 213 (13.77%) 653 (42.21%)
#> Accuracy: 61.41%
#> Sensitivity: 43.61%
#> Specificity: 75.4%
mice_rf_out <- randomForest(formula = factor(retained) ~ .,
data = daacs_train_complete_mice)
mice_rf_predictions <- predict(mice_rf_out, newdata = daacs_valid_complete_mice, type = 'response')
confusion_matrix(observed = daacs_valid_complete_mice$retained,
predicted = mice_rf_predictions)
#> predicted
#> observed FALSE TRUE
#> FALSE 278 (17.97%) 403 (26.05%)
#> TRUE 207 (13.38%) 659 (42.60%)
#> Accuracy: 60.57%
#> Sensitivity: 40.82%
#> Specificity: 76.1%The overall accuracy using only imputed data set is 61.41%
Medley models
The medley function implements a step wise approach to
training models. The data and formula
parameters specify the data set and full model (i.e. all possible
predictor variables to be considered), similar to other modeling
functions in R. The method parameter indicates what model
procedure should be used. In this example we will estimate logistic
regression models. The medley can take any additional
parameters that need to be passed to the method
function.
medley_lr_out <- medley(data = daacs_train,
formula = retained ~ .,
method = glm,
family = binomial(link = logit))#> Warning in predict.medley(medley_lr_out, newdata = daacs_valid, type =
#> "response"): Predictions will be returned from the first model only.Table @ref(tab:model-summaries) provides the baseline retention rate by model along with the number of observations and formula for each of the models. Before exploring the specific of the modeling this reveals that the pattern of missing data is predictive of success. Students who complete all four DAACS assessments are % more likely to be retained then students who did not complete any of the assessments.
| Model | n | Success | Formula |
|---|---|---|---|
| 1 | 1268 | 70.98 | retained ~ page_views + srl + math + reading + writing + income + employment + ell + ed_mother + ed_father + ethnicity + gender + military + age |
| 2 | 788 | 58.25 | retained ~ page_views + srl + income + employment + ell + ed_mother + ed_father + ethnicity + gender + military + age |
| 3 | 1551 | 43.20 | retained ~ income + employment + ell + ed_mother + ed_father + ethnicity + gender + military + age |
The object returned by medley contains the following
elements:
-
n_models- The number of models estimated. -
formulas- A list of the formulas used for each model. -
models- A list containing the model output for each model. In this example this would contain the results of theglmfunction call. -
data- The full data set used to train the models. -
model_observations- A data frame indicating which models each observation was used in. The rows correspond to the rows indataand the columns correspond to the model.
By default the algorithm will use all sets that have at least 10% of
the total observations (see @ref(tab:model-summaries)). This can be
adjusted using the min_set_size parameter (see the
get_variable_sets() function). Optionally you can specify
the models directly by passing a list of formulas with the
var_sets parameter.
Table @ref(tab:modelresults) provides the model summaries for the 3 models estimated.
| (1) | (2) | (3) | ||||
|---|---|---|---|---|---|---|
| (Intercept) | 0.290 | (0.742) | 0.170 | (0.751) | -0.245 | (0.376) |
| page_views | -0.004 | (0.003) | -0.002 | (0.004) | ||
| srl | -0.132 | (0.159) | -0.190 | (0.180) | ||
| math | 0.429 | (0.382) | ||||
| reading | -0.474 | (0.464) | ||||
| writing | 0.153 | (0.425) | ||||
| income | -0.003 | (0.029) | 0.046 | (0.035) | 0.062 * | (0.025) |
| employment | 0.152 | (0.087) | -0.190 | (0.104) | -0.047 | (0.072) |
| ell | 0.034 | (0.268) | 0.436 | (0.318) | 0.311 | (0.210) |
| ed_mother | 0.056 | (0.045) | -0.001 | (0.053) | -0.036 | (0.037) |
| ed_father | 0.011 | (0.044) | 0.093 | (0.052) | 0.024 | (0.036) |
| ethnicityHispanic | -0.241 | (0.251) | 0.438 | (0.264) | 0.123 | (0.186) |
| ethnicityOther | -0.015 | (0.265) | 0.212 | (0.284) | 0.250 | (0.201) |
| ethnicityWhite | 0.053 | (0.198) | 0.348 | (0.194) | 0.069 | (0.134) |
| genderMALE | 0.179 | (0.146) | -0.048 | (0.173) | 0.280 * | (0.120) |
| militaryTRUE | 0.869 *** | (0.155) | 0.643 *** | (0.178) | 0.721 *** | (0.123) |
| age | 0.004 | (0.008) | -0.005 | (0.009) | -0.026 *** | (0.006) |
| N | 1268 | 788 | 1551 | |||
| logLik | -726.090 | -512.952 | -1002.646 | |||
| AIC | 1486.180 | 1053.905 | 2029.291 | |||
| *** p < 0.001; ** p < 0.01; * p < 0.05. | ||||||
The S3 generic function predict has been implemented.
Specifying the newdata parameter will give predictions for
the validation data set.
medley_lr_predictions <- predict(medley_lr_out,
newdata = daacs_valid,
type = 'response')
#> Warning in predict.medley(medley_lr_out, newdata = daacs_valid, type =
#> "response"): Predictions will be returned from the first model only.The confusion matrix is provided below. The overall accuracy for the medley model is 61.086% which is a 5.11% over the baseline, or null, model.
confusion_matrix(observed = daacs_valid$retained,
predicted = medley_lr_predictions > 0.5)
#> predicted
#> observed FALSE TRUE
#> FALSE 305 (19.72%) 376 (24.31%)
#> TRUE 175 (11.31%) 691 (44.67%)
#> Accuracy: 64.38%
#> Sensitivity: 44.79%
#> Specificity: 79.79%Random Forests
The core functionality of the medley algorithm is to
select the most appropriate model given the available data. The specific
predictive model is up to the user. Fernandez-Delgado et al (2014)
evaluated the performance of 179 classifiers across 121 data sets. Their
results showed that, in general, random forest was the best performing
model. To begin, we load the randomForest pacakge and
convert our dependent variable to a factor to ensure a classification
(versus regression) model is estimated.
daacs_train$retained <- as.factor(daacs_train$retained)
daacs_valid$retained <- as.factor(daacs_valid$retained)Training and predicting are the same as above except we set
method = randomForest.
medley_rf_out <- medley(data = daacs_train,
formula = retained ~ .,
method = randomForest)
medley_rf_predictions <- predict(medley_rf_out,
newdata = daacs_valid,
type = "response") == 2
#> Warning in predict.medley(medley_rf_out, newdata = daacs_valid, type =
#> "response"): Predictions will be returned from the first model only.Lastly, the confusion matrix gives the overall accuracy. In this example though we see the random forest performs sligthly worse than logistic regression.
confusion_matrix(observed = daacs_valid$retained,
predicted = medley_rf_predictions )
#> predicted
#> observed FALSE TRUE
#> FALSE 320 (20.69%) 361 (23.34%)
#> TRUE 194 (12.54%) 672 (43.44%)
#> Accuracy: 64.12%
#> Sensitivity: 46.99%
#> Specificity: 77.6%Using observations in multiple models
The default behavior of the medley algorithm is for each
observation to be used in only one model. However, in this particular
example, we have complete demographic data for all students so we could
potentially use all observations to train that model. The
exclusive_membership parameter will allow observations to
be used in training models for which there is complete data.
medley_rf_out2 <- medley(data = daacs_train,
formula = retained ~ .,
exclusive_membership = FALSE,
method = randomForest)
medley_rf_predictions2 <- predict(medley_rf_out2,
newdata = daacs_valid,
type = "response")
confusion_matrix(observed = daacs_valid$retained,
predicted = medley_rf_predictions2 )
#> predicted
#> observed FALSE TRUE
#> FALSE 0 (0.00%) 681 (44.02%)
#> TRUE 0 (0.00%) 866 (55.98%)
#> Accuracy: 55.98%
#> Sensitivity: 0%
#> Specificity: 100%As the results above show we get a very modest increase in the overall accuracy. It should be noted that predictions are estimated from the model that uses most variables for each observation.
Discussion
| Method | Accuracy | Improvement |
|---|---|---|
| Observed data only logistic regression | 61.09 | 4.92 |
| Observed data only random forest | 57.79 | 1.62 |
| Mean imputed data set with logistic regression | 61.15 | 4.98 |
| Mean imputed data set with random forest | 64.90 | 8.73 |
| Mice imputed data set logistic regression | 61.41 | 5.24 |
| Mice imputed data set random forest | 60.57 | 4.40 |
| Medley with logistic regression | 64.38 | 8.21 |
| Medley with random forest | 64.12 | 7.95 |
Note: Improvement is the difference with the overall retention rate of 56.17%.
Predicted
Model Observed FALSE TRUE Accuracy
Observed data only logistic regression FALSE 295 (19.07%) 386 (24.95%)
TRUE 216 (13.96%) 650 (42.02%)
61.09%
Observed data only random forest FALSE 279 (18.03%) 402 (25.99%)
TRUE 251 (16.22%) 615 (39.75%)
57.79%
Imputed data set logistic regression FALSE 297 (19.20%) 384 (24.82%)
TRUE 213 (13.77%) 653 (42.21%)
61.41%
Imputed data set random forest FALSE 278 (17.97%) 403 (26.05%)
TRUE 207 (13.38%) 659 (42.60%)
60.57%
Medley with logistic regression FALSE 305 (19.72%) 376 (24.31%)
TRUE 175 (11.31%) 691 (44.67%)
64.38%
Medley with random forest FALSE 320 (20.69%) 361 (23.34%)
TRUE 194 (12.54%) 672 (43.44%)
64.12%